BOJ - 잘못 구현한 에라토스테네스의 체(15897)
문제(링크)
위 코드에서 반복 횟수는 j의 값에 따라 결정됩니다.
1. 만약 n % j == 0 이라면 n / j 의 값을 결과값에 더해주고, n % j ! = 0 이라면 n / j + 1 의 값을 결과값에 더해주어야 합니다.
하지만 n의 범위가 너무 크므로 횟수를 줄일 방법을 찾아야 합니다.
12 라는 숫자에서, j가 12일 떈 +1을, j 가 6 ~ 11 의 범위 내에선 +2 를 해주면 되고, 4 ~ 5의 범위에선 +3을 해주면 됩니다.
시작 범위(s) > 끝 범위(e) 가 되기 전까지는 위와 같이 계산을 해주면 됩니다.
s > e 부터는 이제 e 까지만 반복문을 수행하면 되므로 시간을 단축할 수 있습니다.
1 ~ e 까지 위 1번 과정을 수행해 줍니다.
124를 계산하면 이런 느낌?입니다.
위 코드에서 반복 횟수는 j의 값에 따라 결정됩니다.
1. 만약 n % j == 0 이라면 n / j 의 값을 결과값에 더해주고, n % j ! = 0 이라면 n / j + 1 의 값을 결과값에 더해주어야 합니다.
하지만 n의 범위가 너무 크므로 횟수를 줄일 방법을 찾아야 합니다.
12 라는 숫자에서, j가 12일 떈 +1을, j 가 6 ~ 11 의 범위 내에선 +2 를 해주면 되고, 4 ~ 5의 범위에선 +3을 해주면 됩니다.
시작 범위(s) > 끝 범위(e) 가 되기 전까지는 위와 같이 계산을 해주면 됩니다.
s > e 부터는 이제 e 까지만 반복문을 수행하면 되므로 시간을 단축할 수 있습니다.
1 ~ e 까지 위 1번 과정을 수행해 줍니다.
124를 계산하면 이런 느낌?입니다.
#include<iostream> #include<algorithm> #include<math.h> #include<string> #include<vector> #include<stack> using namespace std; #define FIO ios_base::sync_with_stdio(false); cin.tie(NULL) #define pii pair<int, int> #define ll long long #define vi vector<int> #define vl vector<long long> #define vii vector<pii> int n; ll ans; int last = 0; int main(void) { FIO; cin >> n; int s = n, e = n, d = 1; while (s <= e) { ans += (e - s + 1) * d; //s ~ e 구간까지의 합을 더함. e = s - 1; d++; s = n / d; if (n % d != 0) s++; } last = e; for (int i = last; i >= 1; i--) { ll r = n / i; if (n % i != 0) r++; ans += r; } cout << ans; }
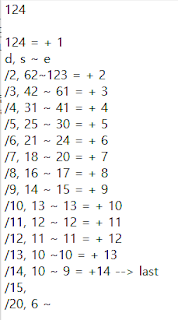


댓글
댓글 쓰기