다익스트라 알고리즘
다익스트라 알고리즘이란?
점과 점 사이의 최단 거리를 구하는 알고리즘으로 한 점에서부터 모든 점까지의 최단 거리를 구할 수 있습니다.
(물론 모든 정점에 대해 다익스트라 알고리즘을 사용하면 모든 점-> 모든점도 가능합니다.)
또한 그리디 기반의 알고리즘이기 때문에 음수 가중치가 있다면 사용이 불가능합니다.
기본적인 아이디어는 다음과 같습니다.
dist[i] 는 시작점 -> i 까지의 거리
1. 시작점을 선택한다.(현재 노드)
2. 연결된 노드(다음 노드)들에 대해 다음 작업을 수행한다.
3. dist[다음 노드] = min(dist[다음 노드] , dist[현재 노드] + 가중치[현재 노드][다음 노드])
4. 연결된 노드 중 시작점과의 거리가 가장 가까운 노드를 현재 노드로 바꾸고 2번부터 수행한다.
위 방법을 이용해 모든 노드에 대한 탐색을 완료하면, 시작점에서 모든 노드에 대한 최단 거리가
dist[] 배열에 담기게 됩니다.
4번째 작업에서 가장 가까운 노드를 뽑는 방법에 따라 시간 복잡도가 변하게 됩니다.
1. 우선순위 큐를 이용한 다익스트라 알고리즘
public static int Dijkstra(int start, int dst){
PriorityQueue<tuple> pq = new PriorityQueue<>(new Comparator<tuple>() {
@Override
public int compare(tuple tuple, tuple t1) {
return tuple.second >= t1.second ? 1 : -1;
}
});
dist = new int[N + 1];
for (int i = 1; i <= N ; i++) {
dist[i] = 1000000000;
}
dist[start] = 0;
pq.offer(new tuple(start, 0));
while(!pq.isEmpty()){
tuple now = pq.poll();
if( now.second > dist[now.first]) continue;
for (int i = 0; i < list.get(now.first).size() ; i++) {
tuple next = list.get(now.first).get(i);
if(dist[next.first] > dist[now.first] + next.second){
dist[next.first] = dist[now.first] + next.second;
pq.offer(new tuple(next.first, dist[next.first]));
}
}
}
return dist[dst];
}
우선순위 큐를 사용한 다익스트라 알고리즘에선 우선순위 큐에 정점의 번호와 시작점에서 그 정점까지의 거리를 tuple로 넣습니다.
우선순위 큐의 정렬을 거리가 짧은 순으로 하게 되면 항상 시작점으로부터 가장 짧은 정점이 나오기 때문에 위의 4번째 작업을 log(V)만에 수행할 수 있습니다.
따라서 정점을 뽑는 log(V) 와 각 정점에 대해 간선을 탐색하므로 E 를 곱해 E * log(V) 의 시간 복잡도를 가집니다.
2. 선형 탐색을 이용한 다익스트라 알고리즘
선형 탐색을 이용한 다익스트라 알고리즘에선 단순히 매번 다음 정점을 정할 때 V번의 선형 탐색을 이용합니다.
따라서 V ^ 2 + E 의 매우 느린 시간 복잡도를 가집니다.
우선순위 큐 VS 선형 탐색
거의 대부분의 경우에 우선순위 큐가 빠르기 때문에 선형 탐색은 많이 쓰이지 않습니다.
하지만 다음과 같이 매우 극단적인 경우에는 선형 탐색이 빠른 경우도 생길 수 있습니다.
V = 4개 , E = 2억개
우선순위 큐 -> E * log(V) = 2억 * log(4) = 4억번
선형 탐색 큐 -> V ^ 2 + E = 4 ^ 2 + 2억 = 2억 16번
즉 정점의 개수가 간선에 비해 극단적으로 적을 때는 선형 탐색이 시간적 이득을 보는 경우가 생기기도 합니다.
- 장점
- 우선순위 큐를 사용하면 최단 경로 알고리즘 중 가장 빠르다.
- 단점
- 음수 가중치가 있다면 사용할 수 없다.
- 구현이 다른 알고리즘에 비해 까다롭다.
연습 문제
특정한 최단 경로(1504)
문제
풀이
함수 Dijkstra(start, end) : return start->end 의 최단 경로
다익스트라 함수를 위와 같이 구현하고
경로1. 1->n1 + n1->n2 + n2->N
경로2. 1->n2 + n2->n1 + n1->N
위 값 중 작은 값을 출력합니다.
코드
import java.io.*;
import java.util.*;
public class Main {
public static int N, E, n1, n2;
public static ArrayList<ArrayList<tuple>> list = new ArrayList<>();
public static int[] dist;
public static boolean flag = true;
public static void main(String[] argc) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
for (int i = 0; i <= N ; i++) {
list.add(new ArrayList<>());
}
for (int i = 0; i < E ; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int d = Integer.parseInt(st.nextToken());
list.get(from).add(new tuple(to, d));
list.get(to).add(new tuple(from, d));
}
st = new StringTokenizer(br.readLine());
n1 = Integer.parseInt(st.nextToken());
n2 = Integer.parseInt(st.nextToken());
int res = Math.min(Dijkstra(1, n1) + Dijkstra(n1, n2) + Dijkstra(n2, N), Dijkstra(1, n2) + Dijkstra(n2, n1) + Dijkstra(n1, N));
if(!flag)
System.out.println(-1);
else
System.out.println(res);
}
public static int Dijkstra(int start, int dst){
PriorityQueue<tuple> pq = new PriorityQueue<>(new Comparator<tuple>() {
@Override
public int compare(tuple tuple, tuple t1) {
return tuple.second >= t1.second ? 1 : -1;
}
});
dist = new int[N + 1];
for (int i = 1; i <= N ; i++) {
dist[i] = 1000000000;
}
dist[start] = 0;
pq.offer(new tuple(start, 0));
while(!pq.isEmpty()){
tuple now = pq.poll();
if( now.second > dist[now.first]) continue;
for (int i = 0; i < list.get(now.first).size() ; i++) {
tuple next = list.get(now.first).get(i);
if(dist[next.first] > dist[now.first] + next.second){
dist[next.first] = dist[now.first] + next.second;
pq.offer(new tuple(next.first, dist[next.first]));
}
}
}
if(dist[dst] == 1000000000)
flag = false;
return dist[dst];
}
}
class tuple {
int first;
int second;
public tuple(int first, int second){
this.first = first;
this.second = second;
}
}
거의 최단 경로(1504)
문제
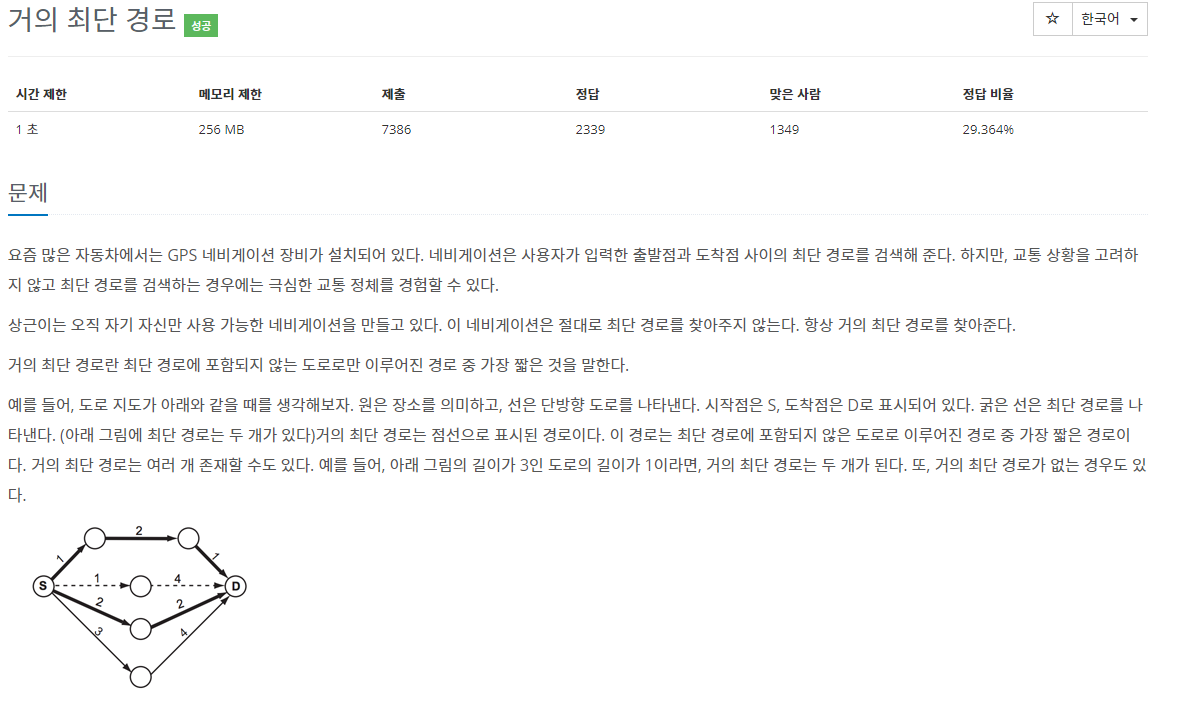

풀이
처음 다익스트라 알고리즘을 사용할 때 최단 경로를 저장하는 prev[][] 인접 행렬을 저장해 줍니다.
(prev[][] 는 종료점부터 시작점까지의 경로를 담고 있습니다.)
다익스트라 알고리즘에서 최단 경로를 찾으면(새로운 최단경로이므로) prev[현재 노드]를 비우고 새로 update합니다.
거리가 같다면, 중복되는 길(여러 갈래길)이므로 prev[현재 노드]에 update만 해줍니다.
그 뒤, BFS를 이용해 prev 인접 행렬을 탐색해가며 반대 방향의 경로를 -1로 바꿔 지워줍니다. 다시 다익스트라 알고리즘을 사용해 거의 최단 경로를 찾습니다.
코드
import java.io.*;
import java.util.*;
public class Main {
public static int N;
public static int min=1000000000;
public static ArrayList<ArrayList<tuple>> list;
public static int[] dist;
public static ArrayList<ArrayList<Integer>> prev;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
while(true) {
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
prev = new ArrayList<>();
if(N==0&&M==0)
break;
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
list = new ArrayList<>();
for (int i = 0; i < N ; i++) {
list.add(new ArrayList<>());
prev.add(new ArrayList<>());
}
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int U = Integer.parseInt(st.nextToken());
int V = Integer.parseInt(st.nextToken());
int P = Integer.parseInt(st.nextToken());
list.get(U).add(new tuple(V, P));
}
Dijkstra(start, end);
delete(end);
int res = Dijkstra(start, end);
if(res != 1000000000)
bw.write( res +"\n");
else
bw.write( -1 +"\n");
}
bw.flush();
bw.close();
}
public static int Dijkstra(int start,int dst){
PriorityQueue<tuple> pq = new PriorityQueue<>(new Comparator<tuple>() {
@Override
public int compare(tuple tuple, tuple t1) {
return tuple.second >= t1.second ? 1 : -1;
}
});
dist = new int[N];
for (int i = 0; i < N ; i++) {
dist[i] = 1000000000;
}
dist[start] = 0;
pq.offer(new tuple(start, 0));
while(!pq.isEmpty()){
tuple now = pq.poll();
if(now.second > dist[now.first]) continue;
for (int i = 0; i < list.get(now.first).size() ; i++) {
tuple next = list.get(now.first).get(i);
if(next.first == -1) continue;
if(dist[next.first] > dist[now.first] + next.second){
dist[next.first] = dist[now.first] + next.second;
pq.offer(new tuple(next.first, dist[next.first]));
prev.get(next.first).clear();
prev.get(next.first).add(now.first);
}
else if(dist[next.first] == dist[now.first] + next.second)
prev.get(next.first).add(now.first);
}
}
return dist[dst];
}
public static void delete(int end){
Queue<Integer> q = new LinkedList<>();
q.offer(end);
while(!q.isEmpty()){
int now = q.poll();
for (int i = 0; i < prev.get(now).size() ; i++) {
int next = prev.get(now).get(i);
for (int j = 0; j < list.get(next).size() ; j++) {
if(list.get(next).get(j).first == now)
list.get(next).get(j).first = -1;
}
q.offer(next);
}
}
}
}
class tuple {
int first;
int second;
public tuple(int first, int second){
this.first = first;
this.second = second;
}
}




댓글
댓글 쓰기