플로이드-와샬 알고리즘
플로이드 와샬 알고리즘이란?
점과 점 사이의 최단 거리를 구하는 알고리즘으로 모든 점에서부터 모든 점까지의 최단 거리를 구할 수 있습니다.
또한 DP 를 이용한 알고리즘이기 때문에 음수 가중치 처리가 가능합니다. (그리디 알고리즘인 다익스트라 알고리즘은 불가능합니다.)
기본적인 아이디어는 다음과 같습니다.
a = 시작점
b = 도착점
c = 거쳐가는 노드
a->b 로의 최단 거리는 a->b 와 a->c->b 중 작은 값
모든 점 c 에 대해 위 작업을 수행하면 모든 점에서의 모든 점까지의 최단 거리를 구할 수 있다.
즉, a 에서 b 로 갈 떄 다른 점(c)을 거쳐가거나 아니면 그대로 갈 지 선택하는 것입니다.
이론에 비해 매우 간단하게 3중 반복문으로 구현할 수 있습니다.
public static void Floid(){
for (int i = 1; i <= N ; i++) {
for (int j = 1; j <= N ; j++) {
for (int k = 1; k <= N ; k++) {
dist[j][k] = Math.min(dist[j][k], dist[j][i] + dist[i][k]);
//dist 배열에서 자기 자신으로 가는 연결은 0, 다른 값들은 최대값(무한)으로 초기화합니다.
}
}
}
}
위 코드에서 dist[j][k] 는 그대로 가는 경로고, dist[j][i] + dist[i][k] 는 i 노드를 거쳐가는 경로입니다.
플로이드 와샬 알고리즘은 O(N^3)의 시간 복잡도로, 최단 거리 알고리즘 중 가장 느립니다.
또한 모든 점 -> 모든 점이기 때문에 공간 복잡도는 O(N^2)이 됩니다.
- 장점
- 음수 가중치를 처리할 수 있다.(사이클이 없다면)
- 모든 점에서의 모든 점까지의 최단 거리를 한번에 구할 수 있다.
- 다른 최단 거리 알고리즘에 비해 구현이 쉽다.
- 단점
- O(N^3)의 시간 복잡도로 가장 느리다.
연습 문제
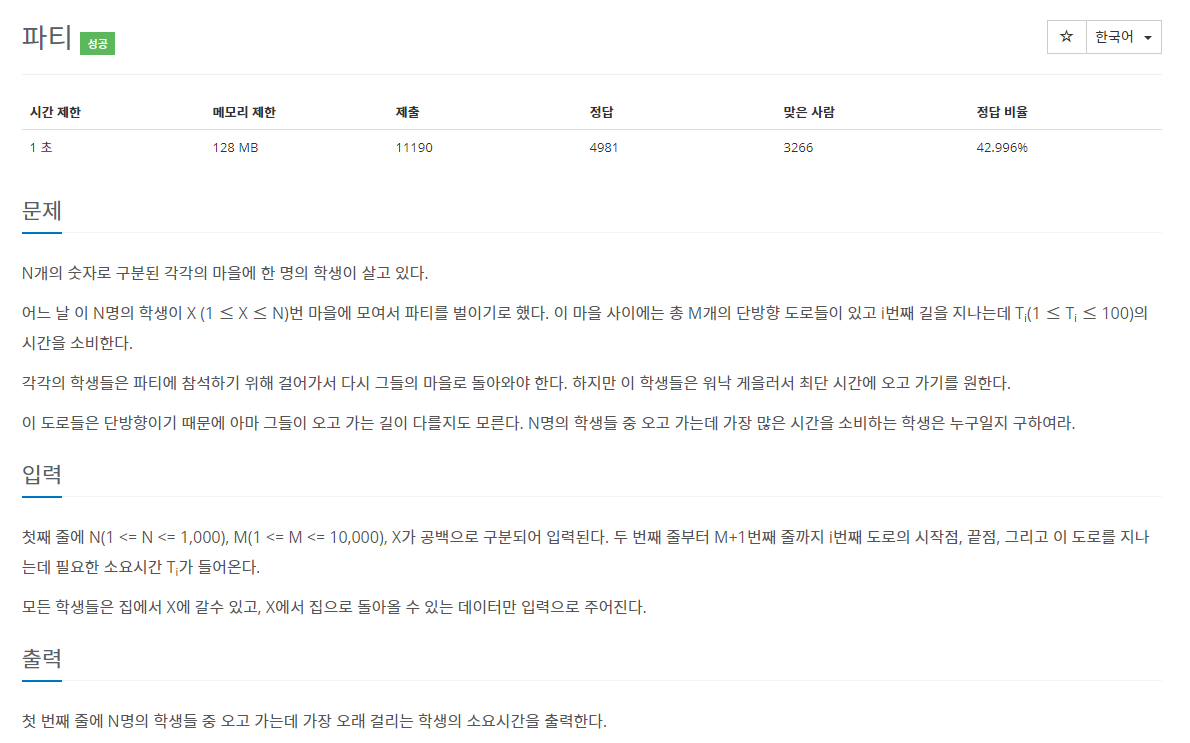
파티(1238)
문제
풀이
플로이드 와샬 기본 문제입니다.
모든 최단 경로를 구하고, 집->X 의 거리 + X->집 의 거리가 최대인 학생을 구합니다.
코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static int N, M, X;
public static int[][] dist;
public static void main(String[] argc) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
X = Integer.parseInt(st.nextToken());
dist = new int[N + 1][N + 1];
for (int i = 0; i <= N ; i++) {
for (int j = 0; j <= N ; j++) {
dist[i][j] = 10000000;
if(i == j)
dist[i][j] = 0;
//자기 자신은 0으로 초기화!
}
}
for (int i = 0; i < M ; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int d = Integer.parseInt(st.nextToken());
dist[from][to] = d;
}
Floid();
int max = 0;
for (int i = 1; i <= N ; i++) {
max = Math.max(max, dist[i][X] + dist[X][i]);
}
bw.write(Integer.toString(max));
bw.flush();
bw.close();
}
public static void Floid(){
for (int i = 1; i <= N ; i++) {
for (int j = 1; j <= N ; j++) {
for (int k = 1; k <= N ; k++) {
dist[j][k] = Math.min(dist[j][k], dist[j][i] + dist[i][k]);
//거리 덧셈에서 오버플로우 조심!
}
}
}
}
}
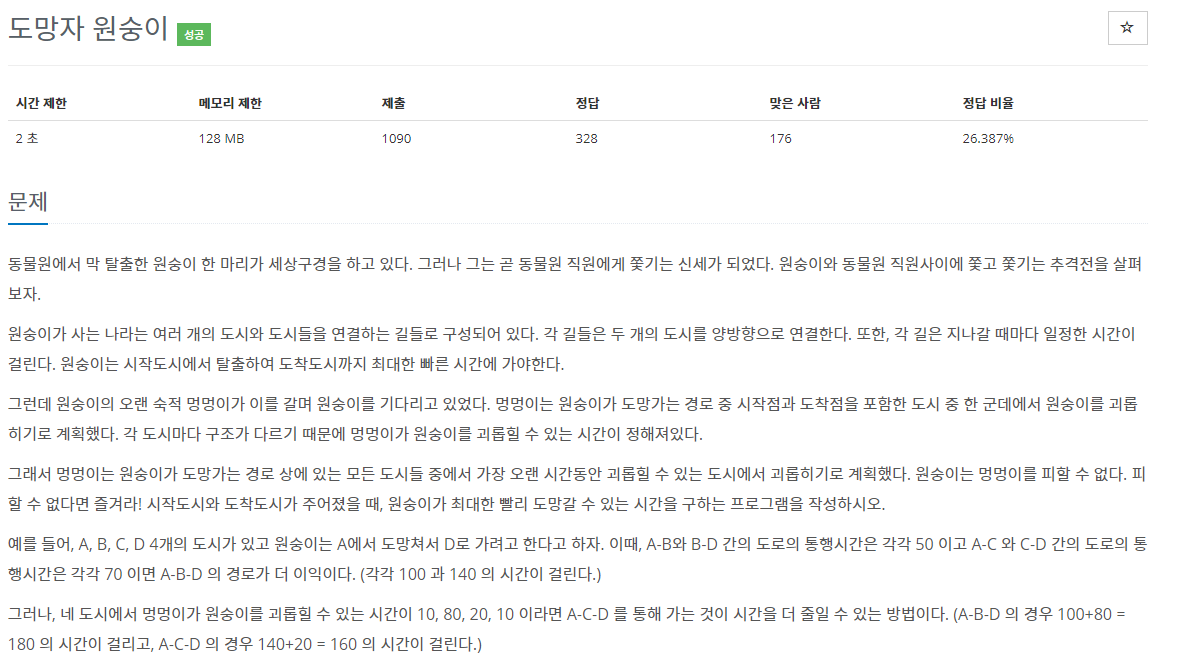
도망자 원숭이(1602)
문제

풀이
각 거리 배열 값은 괴롭히는 시간을 더한 값을 넣어줍니다.
a->b 와 a->c->b 중 더 작은 값을 갱신할 때, a->c 의 괴롭히는 시간 값과 c->b 의 괴롭히는 시간 중 더 큰값으로 비교해 줍니다. 중간 노드인 c 를 비교하는 순서는 괴롭히는 시간이 작은 순서로 비교해주어야 합니다.
코드
import java.io.*;
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Main {
public static int N, M, Q;
public static int[][] dist;
public static int[] city;
public static int[][] plus;
public static PriorityQueue<tuple> pq;
public static void main(String[] argc) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
pq = new PriorityQueue<>(new Comparator<tuple>() {
@Override
public int compare(tuple tuple, tuple t1) {
return tuple.value >= t1.value ? 1 : -1;
}
});
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
Q = Integer.parseInt(st.nextToken());
city = new int[N + 1];
dist = new int[N + 1][N + 1];
plus = new int[N + 1][N + 1];
st = new StringTokenizer(br.readLine());
for (int i = 1; i <= N ; i++) {
city[i] = Integer.parseInt(st.nextToken());
pq.offer(new tuple(i, city[i]));
}
for (int i = 1; i <= N ; i++) {
for (int j = 1; j <= N ; j++) {
plus[i][j] = Math.max(city[i], city[j]);
dist[i][j] = 1000000000;
if(i == j) {
dist[i][j] = 0;
plus[i][j] = 0;
}
}
}
for (int i = 0; i < M ; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int d = Integer.parseInt(st.nextToken());
int p = Math.max(city[a], city[b]);
dist[a][b] = d + p;
dist[b][a] = d + p;
}
Floid();
for (int i = 0; i < Q ; i++) {
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
if(dist[start][end] != 1000000000)
bw.write(dist[start][end] + "\n");
else
bw.write(-1 + "\n");
}
bw.flush();
bw.close();
}
public static void Floid(){
while(!pq.isEmpty()) {
int i = pq.poll().index;
for (int j = 1; j <= N ; j++) {
for (int k = 1; k <= N ; k++) {
if(j == k) continue;
if(i == j || i == k) continue;
int p = Math.max(plus[j][i], plus[i][k]);
if(dist[j][k] > dist[j][i] + dist[i][k] + p - plus[j][i] - plus[i][k]){
//중간 경로 i 가 추가된다.
dist[j][k] = dist[j][i] + dist[i][k] + p - plus[j][i] - plus[i][k];
plus[j][k] = p;
}
}
}
}
}
}
class tuple {
int index;
int value;
public tuple(int index, int value){
this.index = index;
this.value = value;
}
}
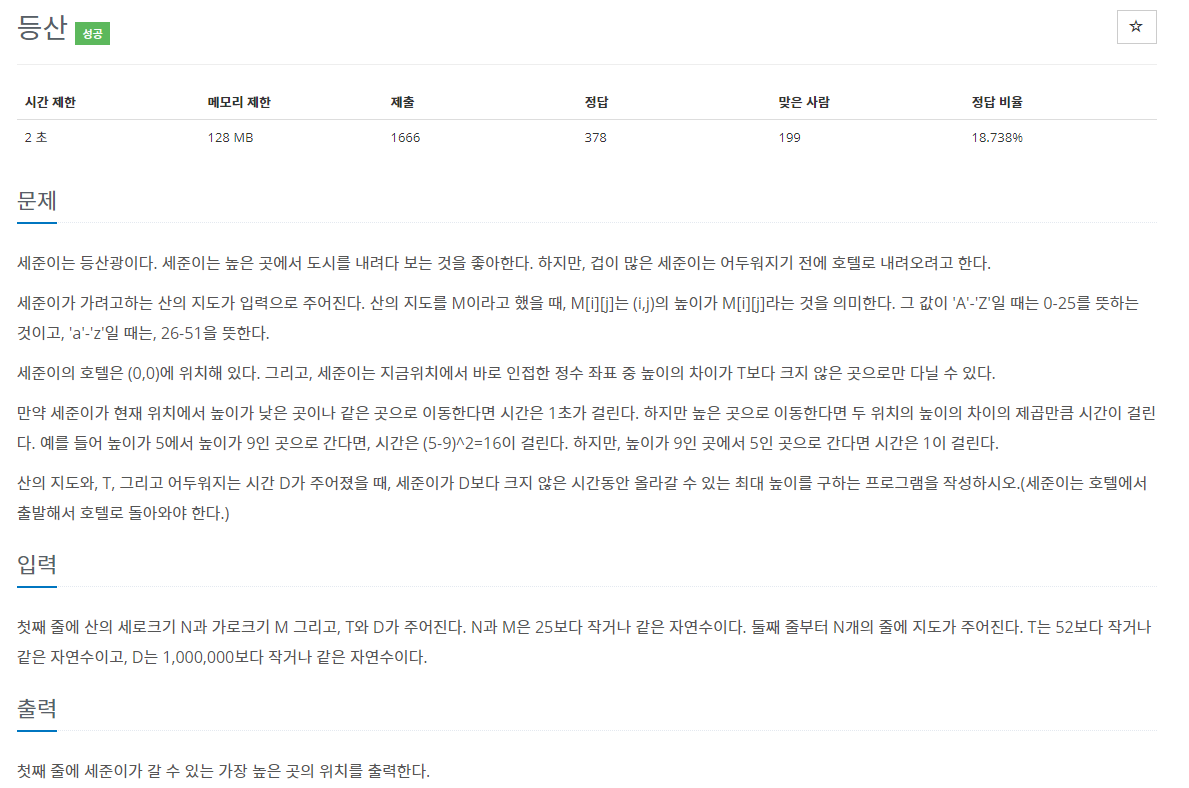
등산(1486)
문제
풀이
총 N M 개의 노드가 생기므로 플로이드 와샬 알고리즘을 위해 dist[N M][N * M] 의 배열을 만듭니다. map의 모든 점에 대하여 상하좌우에 대한 간선에 가중치를 부여합니다.(차의 절대값이 T보다 크면 연결하지 않습니다.) 플로이드 와샬 알고리즘으로 모든 점에 대한 최단 거리를 구하고 (0,0)으로 돌아올 수 있는 값 == dist[0][x] + dist[x][0] <= D 중 최대값을 구합니다.
점의 좌표에 따라 노드의 인덱스를 다음과 같이 찾아줍니다.(4x4 배열)
0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15
가로의 길이를 M 이라 하면, 점(i,j) 의 인덱스는 i * M + j 입니다.
인덱스로 점의 좌표를 찾는 방법도 반대로 하면 됩니다.
코드
import java.io.*;
import java.util.*;
public class Main {
public static int N, M, T, D;
public static int[][] map;
public static int[][] dist;
public static int[] dir1 = {0,0,1,-1};
public static int[] dir2 = {1,-1,0,0};
public static void main(String[] argc) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
T = Integer.parseInt(st.nextToken());
D = Integer.parseInt(st.nextToken());
map = new int[N][M];
dist = new int[N * M][N * M];
for (int i = 0; i < N * M; i++) {
for (int j = 0; j < N * M ; j++) {
dist[i][j] = 1000000000;
if(i == j)
dist[i][j] = 0;
}
}
for (int i = 0; i < N ; i++) {
String str = br.readLine();
for (int j = 0; j < M ; j++) {
char c = str.charAt(j);
if(c >= 'A' && c <= 'Z')
map[i][j] = c - 'A';
else
map[i][j] = c - 'a' + 26;
}
}
for (int i = 0; i < N ; i++) {
for (int j = 0; j < M ; j++) {
for (int k = 0; k < 4 ; k++) {
XY next = new XY(i + dir1[k], j + dir2[k]);
if(next.x < 0 || next.x >= N || next.y < 0 || next.y >= M) continue;
int now_Node = i * M + j;
int next_Node = next.x * M + next.y;
if(Math.abs(map[i][j] - map[next.x][next.y]) > T) continue;
if(map[i][j] < map[next.x][next.y]){
dist[now_Node][next_Node] = (int)Math.pow(Math.abs(map[i][j] - map[next.x][next.y]), 2);
}
else{
dist[now_Node][next_Node] = 1;
}
}
}
}
Floid();
int max = 0;
for (int i = 0; i < N * M ; i++) {
if(dist[0][i] + dist[i][0] <= D)
max = Math.max(max, map[i / M][i % M]);
}
bw.write(Integer.toString(max));
bw.flush();
bw.close();
}
public static void Floid(){
for (int i = 0; i < N * M ; i++) {
for (int j = 0; j < N * M ; j++) {
for (int k = 0; k < N * M ; k++) {
dist[j][k] = Math.min(dist[j][k], dist[j][i] + dist[i][k]);
}
}
}
}
}
class XY {
int x;
int y;
public XY(int x, int y){
this.x = x;
this.y = y;
}
}





댓글
댓글 쓰기